Serie de Laplace
_-_Gu%C3%A9rin.jpg/250px-Pierre-Simon,_marquis_de_Laplace_(1745-1827)_-_Gu%C3%A9rin.jpg)
Es un procedimiento desarrollado por el matemático y
astrónomo francés Pierre Simón Marques de Laplace (1749 - 1827) que permite
cambiar funciones de la variable del tiempo (t) a una función de la variable
compleja (s).
El Método de la transformada de Laplace es un método
operacional que puede usarse para resolver ecuaciones diferenciales lineales.
Con el uso de la transformada de Laplace muchas funciones sinusoidales y
exponenciales, se pueden convertir en funciones algebraicas de una variable
compleja (s), y reemplazar operaciones como la diferenciación y la
integración, por operaciones algebraicas en el plano complejo.
La transformada de Laplace de una función f (t) para todos los números positivos t ≥ 0, es la función F(s), definida por:
Propiedades
Linealidad
se verifica
Cambio de Escala
Desplazamiento en frecuencia
Desplazamiento en el Tiempo
u(t) es la función escalón unitario
Desplazamiento n-ésima
Convolución
Derivación
Integración
Dualidad
Transformada de Laplace de una función con periodo p
Teorema del valor inicial
Teorema de valor final
Teorema del valor final aporta
información cualitativa de la Transformada de Laplace en conexión directa con
la función de la cual es transformada.
para mas información acerca de los teoremas de Laplace aquí les dejo este enlace
http://www.dmae.upct.es/~jose/varcomp/ctrans.pdf
Tabla con Transformadas de Laplace
Tabla con las Transformadas Inversas de Laplace
Serie de Fourier
El nombre se debe al matemático francés Jean-Baptiste Joseph Fourier que
desarrolló la teoría cuando estudiaba la ecuación del calor. Fue el
primero que estudió tales series sistemáticamente, y publicando sus resultados
iniciales en 1807 y 1811. Esta área de investigación se llama
algunas veces Análisis armónico.
Las series de Fourier surgen de la
tarea practica de representar una función periódica f(x) en términos de funciones
seno y coseno. La razón se debe a la facilidad con la que se resuelven ciertos problemas
cuando se transforman estas funciones periódicas en series de Fourier.
La serie de Fourier tiene la forma:
Donde an y bn se denominan coeficientes de
Fourier de la serie de Fourier de la función f(x).
La serie de Fourier
de una función par de periodo 2L es una serie de Fourier de cosenos.
con coeficientes:
Función Impar
La serie de Fourier
de una función impar de periodo 2L es una serie de Fourier de senos.
con coeficientes:
aquí les dejo un enlace para mas contenido acerca de la Serie de Fourier
http://webdelprofesor.ula.ve/ingenieria/derivas/apuntes_del_postgrado/pres_seriesdefourier.pdf
Tabla con las Transformadas de Fourier
Ejercicios resueltos Transformada de Laplace y Series de Fourier
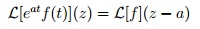
No hay comentarios:
Publicar un comentario